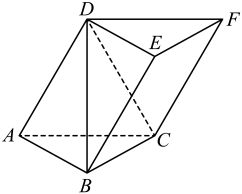
1.
如图,在三角锥  中,
中,  ,
,  ,
,  为
为  的中点.
的中点.
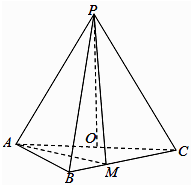
(1)
证明:  平面
平面  ;
(2)
若点
;
(2)
若点  在棱
在棱  上,且二面角
上,且二面角  为
为  ,求
,求  与平面
与平面  所成角的正弦值.
所成角的正弦值.
【考点】
直线与平面垂直的性质;
直线与平面所成的角;
二面角及二面角的平面角;