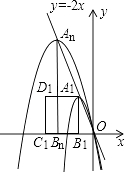
定义：对于关于的函数，函数在范围内有最大值和最小值，则称为极差值，记作．如函数，在范围内，该函数的最大值是4，最小值为，即．请根据以上信息，完成下列问题：

1. 定义：对于 $\text{[math]}$ 关于 $\text{[math]}$ 的函数，函数在 $\text{[math]}$ 范围内有最大值 $\text{[math]}$ 和最小值 $\text{[math]}$ ，则 $\text{[math]}$ 称为极差值，记作 $\text{[math]}$ ．如函数 $\text{[math]}$ ，在 $\text{[math]}$ 范围内，该函数的最大值是4，最小值为 $\text{[math]}$ ，即 $\text{[math]}$ ．请根据以上信息，完成下列问题：

(1) 已知二次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ．

①求该函数的表达式；

②求该函数的 $\text{[math]}$ 的值．

(2) 已知函数 $\text{[math]}$ ，函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ，且两个函数的 $\text{[math]}$ 相等，求 $\text{[math]}$ 的值．

【考点】

待定系数法求二次函数解析式; 一次函数的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 已知二次函数 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ ．

(1) 求 $\text{[math]}$ ， $\text{[math]}$ 的值．

(2) 当 $\text{[math]}$ 时，求函数 $\text{[math]}$ 的值．

(3) 请直接写出当 $\text{[math]}$ ， $\text{[math]}$ 的取值范围．

解答题普通

2. 在平面直角坐标系中，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ 、 $\text{[math]}$ ．

(1) 求这条抛物线所对应的函数表达式；

(2) 求这条抛物线的开口方向和顶点坐标．

解答题普通

3. 北方的冬天，人们酷爱冰雪运动，在这项运动里面，我们可以用数学知识解决一些实际问题．如图是某跳台滑雪训练场的横截面示意图，取某一位置的水平线为x轴，过跳台终点A作水平线的垂线为y轴，建立平面直角坐标系如图所示，图中的抛物线 $\text{[math]}$ 近似表示滑雪场地上的一座小山坡，某运动员从点O正上方50米处的A点滑出，滑出后沿一段抛物线 $\text{[math]}$ 运动．当运动员运动到离A处的水平距离为60米时，离水平线的高度为60米．

(1) 求小山坡最高点到水平线的距离．

(2) 求抛物线 $\text{[math]}$ 所对应的函数表达式．

(3) 当运动员滑出点A后，直接写出运动员运动的水平距离为多少米时，运动员与小山坡 $\text{[math]}$ 的竖直距离为10米．

解答题困难