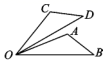
1.
如图,在 ,
,  中,
中, ,
,  ,
,  , C,D,E三点在同一直线上,连接
, C,D,E三点在同一直线上,连接 , 以下四个结论
, 以下四个结论

①;②
;
③;④
.
其中结论正确的是.(把正确结论的序号填在横线上).
【考点】
三角形全等的判定-SAS;
基础巩固
能力提升
变式训练
拓展培优
真题演练