1.
定义:在平面直角坐标系 中,对于
中,对于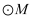 内的一点
内的一点 , 若在
, 若在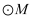 外存在点
外存在点 , 使得
, 使得 , 则称点
, 则称点 为
为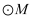 的“内半点”.
的“内半点”.

(1)
当 的半径为
的半径为 时,
(2)
已知点
时,
(2)
已知点 ,
,  ,
,  ,
, 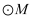 的半径为
的半径为 , 若线段
, 若线段 上存在
上存在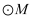 的“内半点”,直接写出
的“内半点”,直接写出 的取值范围.
的取值范围.
①在点 ,
,
中,是
的“内半点”的是_______;
②已知一次函数 , 若一次函数在第一象限的图象上的所有点都是
的“内半点”,求k的取值范围;
【考点】
解一元一次不等式组;
圆的相关概念;
坐标系中的两点距离公式;
能力提升