1.
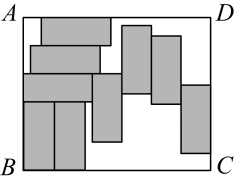
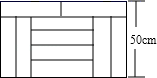
小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图1;小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图2那样的正方形,中间还留下了一个洞,恰好是边长为 的小正方形,则每个小长方形的面积为( )
的小正方形,则每个小长方形的面积为( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
二元一次方程组的应用-几何问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练