1.
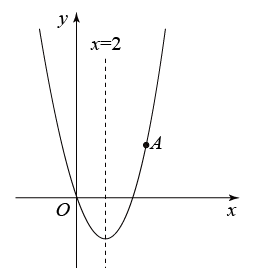
已知抛物线 经过点
经过点 ,
,  ,
,  , 连接
, 连接 、
、 , 令
, 令 .
.
(1)
若 ,
,  , 求
, 求 的值;
(2)
若
的值;
(2)
若 ,
,  , 求a的值.
, 求a的值.
【考点】
坐标系中的两点距离公式;