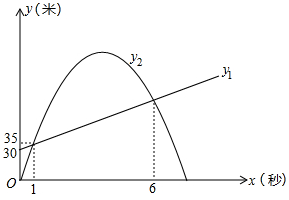
某航模小组研制了一种航模飞机，为了测试航模飞机的性能，飞机从水平放置的圆柱形发射台的上底面中心处起飞，其飞行轨迹是一条抛物线．以发射台的下底面中心为坐标原点，过原点的水平线为轴，所在直线为轴，建立如图所示的平面直角坐标系．若发射台的高度为，测得当飞行的水平距离为时，飞机的飞行高度为；当飞行的水平距离为时，飞机的飞行高度为．

0 返回首页

1. 某航模小组研制了一种航模飞机，为了测试航模飞机的性能，飞机从水平放置的圆柱形发射台的上底面中心 $\text{[math]}$ 处起飞，其飞行轨迹是一条抛物线．以发射台的下底面中心 $\text{[math]}$ 为坐标原点，过原点的水平线为 $\text{[math]}$ 轴， $\text{[math]}$ 所在直线为 $\text{[math]}$ 轴，建立如图所示的平面直角坐标系．若发射台的高度 $\text{[math]}$ 为 $\text{[math]}$ ，测得当飞行的水平距离为 $\text{[math]}$ 时，飞机的飞行高度为 $\text{[math]}$ ；当飞行的水平距离为 $\text{[math]}$ 时，飞机的飞行高度为 $\text{[math]}$ ．

(1) 求抛物线的解析式．

(2) 求飞机飞行的最大高度及最远距离．

(3) 由于发射台可以上下升降，保证其他起飞条件不变的前提下，抛物线随着起飞点 $\text{[math]}$ 的上下平移而上下平移．如图，在水平线 $\text{[math]}$ 轴上设置回收区域 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，要使飞机恰好降落到 $\text{[math]}$ 内（包括端点 $\text{[math]}$ ， $\text{[math]}$ ），直接写出发射台的高度 $\text{[math]}$ 的取值范围．

【考点】

二次函数的实际应用-抛球问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通