1.
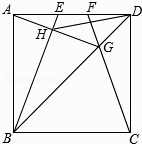
如图1,矩形 中,
中, ,
,  ,
,  为矩形
为矩形 的对角线,
的对角线, 的平分线交
的平分线交 的延长线于点
的延长线于点 . 点
. 点 是线段
是线段 上的动点,以
上的动点,以 为对角线作正方形
为对角线作正方形 (点
(点 ,
,  ,
,  ,
,  按逆时针方向排列).
按逆时针方向排列).

(1)
求 的长;
(2)
如图2,若点G落在
的长;
(2)
如图2,若点G落在 边上,求
边上,求 的值;
(3)
在点F的运动过程中,是否存在某一位置,使得正方形
的值;
(3)
在点F的运动过程中,是否存在某一位置,使得正方形 的某边落在
的某边落在 的一边上?若存在,直接写出
的一边上?若存在,直接写出 的长?若不存在,请说明理由.
的长?若不存在,请说明理由.
【考点】
正方形的性质;
相似三角形的判定与性质;
解直角三角形;