1.
两个顶角相等的等腰三角形,如果具有公共的顶角顶点,并将它们的底角顶点分别对应连接起来得到两个全等三角形,我们把这样的图形称为“手拉手”图形.

(1)
如图1,在“手拉手”图形中, , 若
, 若 , 则
, 则
 (2)
如图2,
(2)
如图2, 和
和 是等边三角形,连接
是等边三角形,连接 ,
,  交于点O,求
交于点O,求 的度数;
(3)
如图3,
的度数;
(3)
如图3, ,
,  , 试探究
, 试探究 与
与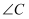 的数量关系.
的数量关系.
【考点】
三角形内角和定理;
等边三角形的判定与性质;
三角形全等的判定-SAS;
能力提升



