在等腰Rt△ABC中，AB＝AC ， ∠BAC＝90°．

1. 在等腰Rt△ABC中，AB＝AC ， ∠BAC＝90°．

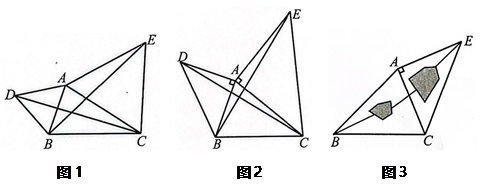
(1) 如图1，D ， E是等腰Rt△ABC斜边BC上两动点，且∠DAE＝45°，在等腰Rt△ABC外侧作△CAF≌△BAE ，连接DF ．

问：①∠DCF＝ °．

②△AED与△AFD是否全等？请说明理由；

③当BE＝3，CE＝7时，求DE的长；

(2) 如图2，点D是等腰Rt△ABC斜边BC所在射线CB上的一动点，连接AD ，以点A为直角顶点作等腰Rt△ADE（点E在点D的顺时针方向上），当BD＝4，BC＝12时，直接写出DE的长．（画出图形，做必要标记，不必写过程）．

【考点】

勾股定理; 等腰直角三角形; 三角形全等的判定-SAS; 三角形的综合;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图1，已知 $\text{[math]}$ ，以 $\text{[math]}$ 、 $\text{[math]}$ 为边分别向 $\text{[math]}$ 外作等边 $\text{[math]}$ 和等边 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，则有 $\text{[math]}$ .

(1) 如图2，已知 $\text{[math]}$ ，以 $\text{[math]}$ 、 $\text{[math]}$ 为边分别向外作等腰直角三角形 $\text{[math]}$ 和等腰直角三角形 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，猜想 $\text{[math]}$ 与 $\text{[math]}$ 有什么数量关系？并说明理由.

(2) 如图2，连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值.

(3) 运用图（1），图（2）中所积累的经验和知识，完成下题：如图（3），要测量池塘两岸相对的两点B、E的距离，已经测得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 米， $\text{[math]}$ ，求 $\text{[math]}$ 的长（结果保留根号）.

综合题困难

2. 如图，△ABC和△DCE都是等腰直角三角形，CA＝CB，CD＝CE，且点D在△ABC的斜边AB上．

(1) 连结AE，求证：△ACE≌△BCD．

(2) 若BD＝2，CD＝6，求AD的长．

综合题普通

3. 已知△ABC和△ADE都是等腰直角三角形，点D是直线BC上的一动点（点D不与B，C重合），连接CE.

(1) 在图1中，当点D在边BC上时，求证：BC=CE+CD；

(2) 在图2中，当点D在边BC的延长线上时，结论BC=CE+CD是否还成立？若不成立，请猜想BC，CE， CD之间存在的数量关系，并说明理由；

(3) 在图3中，当点D在边BC的反向延长线上时，不需写证明过程，直接写出BC，CE， CD之间存在的数量关系及直线CE与直线BC的位置关系.

综合题困难