1.
如图1,已知 , 以
, 以 、
、 为边分别向
为边分别向 外作等边
外作等边 和等边
和等边 , 连接
, 连接 、
、 , 则有
, 则有 .
.
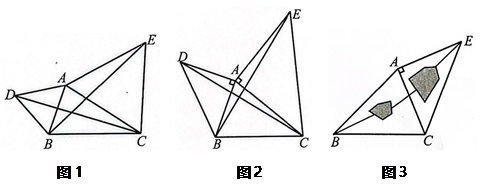
(1)
如图2,已知 , 以
, 以 、
、 为边分别向外作等腰直角三角形
为边分别向外作等腰直角三角形 和等腰直角三角形
和等腰直角三角形 , 连接
, 连接 、
、 , 猜想
, 猜想 与
与 有什么数量关系?并说明理由.
(2)
如图2,连接
有什么数量关系?并说明理由.
(2)
如图2,连接 , 若
, 若 ,
,  ,
,  , 求
, 求 的值.
(3)
运用图(1),图(2)中所积累的经验和知识,完成下题:如图(3),要测量池塘两岸相对的两点B、E的距离,已经测得
的值.
(3)
运用图(1),图(2)中所积累的经验和知识,完成下题:如图(3),要测量池塘两岸相对的两点B、E的距离,已经测得 ,
,  ,
,  米,
米, , 求
, 求 的长(结果保留根号).
的长(结果保留根号).
【考点】
等腰直角三角形;
三角形全等的判定-SAS;
三角形的综合;
能力提升




