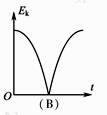
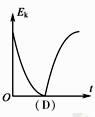
1.
某同学让小球从距地面高度为 处竖直向上抛出,开始
处竖直向上抛出,开始 内上升的高度与最后
内上升的高度与最后 内上升的高度之比为
内上升的高度之比为 , 不计空气阻力,重力加速度大小为
, 不计空气阻力,重力加速度大小为 , 求:
, 求:
(1)小球最初的平均速度
大小;
(2)小球上升到最高点离地面的高度H。

【考点】
竖直上抛运动;