1.
我们知道: , 由此我们给出如下定义:对于给定的一次函数y=kx+b(k、b为常数且k≠0),把形如
, 由此我们给出如下定义:对于给定的一次函数y=kx+b(k、b为常数且k≠0),把形如 k、b为常数且k≠0)的函数称为一次函数y=kx+b的演变函数.
k、b为常数且k≠0)的函数称为一次函数y=kx+b的演变函数.
(1)
已知函数y=2x+1.
(2)
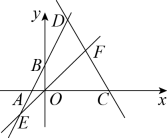
如图,一次函数y=kx+b(k≠0,k、b为常数)的演变函数图象与一次函数 的图像相交于A(-3 , p)、B(2 , q)两点,
的图像相交于A(-3 , p)、B(2 , q)两点,
①若点E(﹣1,m)在这个一次函数的演变函数图象上,则m=;
②若点F(n , 3)在这个一次函数的演变函数图象上,则n=.

①求该一次函数的表达式.
②一次函数y=kx+b(k≠0,k、b为常数)的演变函数图象与y轴相交于点C , 求△ABC的面积.
③在一次函数y=kx+b(k≠0,k、b为常数)的演变函数图象是否存在点P,使得PA=PB , 若存在,请直接写出点P的坐标;若不存在,请说明理由.
【考点】
待定系数法求一次函数解析式;
两一次函数图象相交或平行问题;
一次函数的性质;
一次函数中的面积问题;
能力提升