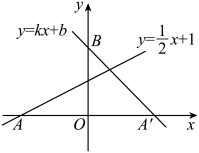
在平面直角坐标系中，抛物线与y轴交于点A，其对称轴与x轴交于点B，一次函数的图象经过点A，B．

1. 在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 与y轴交于点A，其对称轴与x轴交于点B，一次函数 $\text{[math]}$ 的图象经过点A，B．

(1) 求一次函数的表达式；

(2) 当 $\text{[math]}$ 时，对于x的每一个值，函数 $\text{[math]}$ 的值大于一次函数 $\text{[math]}$ 的值，直接写出n的取值范围．

【考点】

待定系数法求一次函数解析式; 两一次函数图象相交或平行问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 经研究表明，某市跨河大桥上的车流速度 $\text{[math]}$ （单位：千米/时）是车流密度 $\text{[math]}$ （单位：辆/千米）的函数，函数图象如图所示.

(1) 当 $\text{[math]}$ 时， $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式是______；

(2) 求车流量 $\text{[math]}$ （单位：辆/时）与车流密度 $\text{[math]}$ 之间的函数关系式；（注：车流量是单位时间内通过观测点的车辆数，计算公式为：车流量＝车流速度×车流密度）

(3) 若车流速度 $\text{[math]}$ 不低于50千米/时，求当车流密度 $\text{[math]}$ 为多少时，车流量 $\text{[math]}$ 达到最大，并求出这一最大值.

综合题普通

2. 如图，直线 $\text{[math]}$ 与x轴、y轴分别交于 $\text{[math]}$ 、B两点，与直线 $\text{[math]}$ ： $\text{[math]}$ 交于点D，且 $\text{[math]}$ 的面积为15.

(1) 求直线 $\text{[math]}$ 的解析式；

(2) 直线 $\text{[math]}$ 经过原点，与直线 $\text{[math]}$ 交于点E，与直线 $\text{[math]}$ 交于点F，若E点的横坐标为 $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积.

综合题普通

3. 如图，一次函数y＝x＋3的图象 $\text{[math]}$ 与x轴交于点B，与过点A（3，0）的一次函数的图象 $\text{[math]}$ 交于点C（1，m）.

(1) 求m的值；

(2) 求一次函数图象 $\text{[math]}$ 相应的函数表达式；

(3) 求 $\text{[math]}$ 的面积.

综合题普通