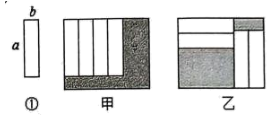
1.
把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为3a厘米,宽为(2a-b)厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.

(1)求大长方形ABCD的周长;
(2)求图②中两块阴影部分周长之和.(用含a,b的式子表示)
【考点】
整式的加减运算;
用代数式表示几何图形的数量关系;
基础巩固
能力提升
变式训练
拓展培优