1.
已知 , 猜想
, 猜想 与
与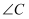 的关系如何?并说明理由.
的关系如何?并说明理由.

解:因为(已知)
所以(______)
所以;
同理,;
所以______(______).
【考点】
余角、补角及其性质;
平行线的判定与性质;












