1.
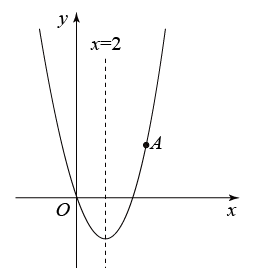
二次函数 的图象经过点
的图象经过点 ,
,  , 且最低点的纵坐标为
, 且最低点的纵坐标为 .
.
(1)
求 ,
,  和
和 的值;
(2)
若直线
的值;
(2)
若直线 经过点
经过点 , 求
, 求 的值;
(3)
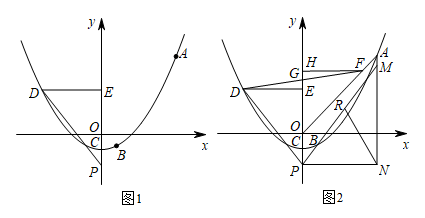
记(1)中的二次函数图象在点
的值;
(3)
记(1)中的二次函数图象在点 ,
,  之间的部分图象为
之间的部分图象为 (包含
(包含 ,
,  , 两点),若直线
, 两点),若直线 与
与 有公共点,请结合图象探索实数
有公共点,请结合图象探索实数 的取值范围.
的取值范围.
【考点】
待定系数法求一次函数解析式;
待定系数法求二次函数解析式;
能力提升
真题演练