1.
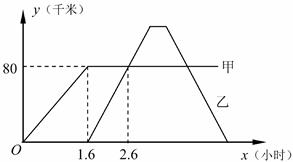
某快递公司每天上午9:00-10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示.

(1)
求甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数表达式.
(2)
求两直线的交点坐标,并说明其含义.
【考点】
一次函数的实际应用;