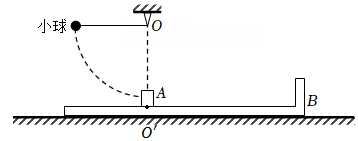
如图所示，在广阔的水平面上固定有一个边长为的正方形光滑薄板ABCD，薄板中心O点钉有一枚钉子，长为L的不可伸长的轻绳一端通过极小绳套套在钉子上，另一端与质量为m的物块P连接，物块以大小为v0的速度绕O点做圆周运动。不计绳套与钉子间的摩擦力，重力加速度取g。求：

1. 如图所示，在广阔的水平面上固定有一个边长为 $\text{[math]}$ 的正方形光滑薄板ABCD，薄板中心O点钉有一枚钉子，长为L的不可伸长的轻绳一端通过极小绳套套在钉子上，另一端与质量为m的物块P连接，物块以大小为v₀的速度绕O点做圆周运动。不计绳套与钉子间的摩擦力，重力加速度取g。求：

(1) 物块P运动到图中M点（ $\text{[math]}$ ）时，绳子张力T的大小；

(2) 某时刻剪断轻绳，从剪断轻绳到物块P离开薄板的最短时间t；

(3) 在（2）的结果下，将物块离开薄板的位置标记为N点（图中未画出），沿着离开时的速度方向，从N点前方Q点（图中未画出）开始每间距L静置有与P完全相同的物块很多个（N、Q间距也为L），将Q点静置的物块编号为1，以后依次为2、3、4……，在物块P到达N点时立即对其施加与速度同向的恒力 $\text{[math]}$ 物块与水平面间的动摩擦因数均为 $\text{[math]}$ 所有物块间的碰撞均为完全非弹性碰撞。则最多能与编号为多少的滑块相碰撞。

【考点】

动量守恒定律; 碰撞模型;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 如图所示，光滑水平地面上静置一表面光滑的 $\text{[math]}$ 圆弧凹槽D和一长木板C，质量均为m=1kg，木板与凹槽紧挨，木板上表面与凹槽圆弧表面相切。上方H=1.8m处有一长L₁=5m的水平传送带以v=8m/s的速度顺时针运行，将一质量m₁=1kg的小物块P（可视为质点）轻放在传送带的左端，物块与传送带的动摩擦因数μ₁=0.8，P离开传送带后，落至木板表面无反弹，竖直方向速度经 $\text{[math]}$ 减为0，此时物块P离木板右端长度为L₂=3.5m，物块与木板表面动摩擦因数μ₂=0.2，物块到达木板右端后冲上凹槽，圆弧表面半径R=0.2m，g取10m/s² ，求：

(1) 物块离开传送带时的速度大小v₁及刚接触木板的速度大小v₂；

(2) 物块经 $\text{[math]}$ 作用后，物块速度v₃及木板速度v₄的大小；

(3) 判断物块滑上凹槽后能否从上端离开，如果能，求离开后还能上升的高度；如果不能，求物块滑上凹槽后上升的最大高度。

解答题困难

2. 如图所示，质量为m_B=4kg的平板小车B和质量为m_C=2kg的平板小车C紧挨着一起静止于光滑水平面上（两车不粘连），两小车上表面高度相同并平滑相接。平板小车B最左端放置有质量为m_A=2kg的小物块A（可视为质点），已知小物块A与平板小车B之间的动摩擦因数为μ=0.1，平板小车B足够长，小物块A总不能到平板小车B的右端。平板小车C的最右端固定一竖直轻杆，杆顶系一长为R=1.8m的轻绳，轻绳的另一端系一质量为m=1kg的小球（可视为质点）。某时刻，轻绳被水平拉直处于静止状态，小球处于最左端，将小球由静止释放，求：（重力加速度g=10m/s²）

(1) 当小斑摆到最低点时，平板小车C移动的距离；

(2) 将平板小车C固定，在平板小车B右侧水平面上与平板小车B右端相距L处固定一竖直弹性挡板，平板小车B碰撞挡板时间极短，碰撞后速度大小不变、方向反向，已知小球摆到最低点时恰好与小物块A发生的碰撞为一维弹性碰撞，求；

①小球与小物块A发生碰撞后瞬间，小物块A的速度v_A大小；

②要使平板小车B与挡板至少发生n次碰撞，L应满足的条件。

解答题困难

3. 如图所示，木板A、B静止于光滑水平桌面上，B上表面水平且足够长，其左端放置一滑块C，B、C间的动摩擦因数为μ，A、B由不可伸长的理想轻绳连接，绳子处于松弛状态，现在突然给C一个向右的速度2v₀ ，让C在B上滑动，当C的速度为v₀时，绳子刚好伸直，接着绳子被瞬间拉断，绳子拉断时B的速度为 $\text{[math]}$ ， A、B、C的质量均为m。

（1）从C获得速度2v₀开始经过多长时间绳子被拉直？

（2）拉断绳子造成的机械能损失为多少？

（3）若最终滑块C未脱离木板B，则木板B的长度至少为多少？

解答题困难