1.
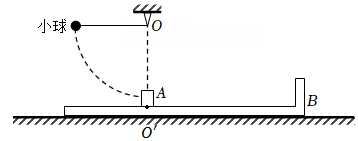
如图所示,质量为mB=4kg的平板小车B和质量为mC=2kg的平板小车C紧挨着一起静止于光滑水平面上(两车不粘连),两小车上表面高度相同并平滑相接。平板小车B最左端放置有质量为mA=2kg的小物块A(可视为质点),已知小物块A与平板小车B之间的动摩擦因数为μ=0.1,平板小车B足够长,小物块A总不能到平板小车B的右端。平板小车C的最右端固定一竖直轻杆,杆顶系一长为R=1.8m的轻绳,轻绳的另一端系一质量为m=1kg的小球(可视为质点)。某时刻,轻绳被水平拉直处于静止状态,小球处于最左端,将小球由静止释放,求:(重力加速度g=10m/s2)

(1)
当小斑摆到最低点时,平板小车C移动的距离;
(2)
将平板小车C固定,在平板小车B右侧水平面上与平板小车B右端相距L处固定一竖直弹性挡板,平板小车B碰撞挡板时间极短,碰撞后速度大小不变、方向反向,已知小球摆到最低点时恰好与小物块A发生的碰撞为一维弹性碰撞,求;
①小球与小物块A发生碰撞后瞬间,小物块A的速度vA大小;
②要使平板小车B与挡板至少发生n次碰撞,L应满足的条件。
【考点】
动量守恒定律;
碰撞模型;
能力提升
真题演练