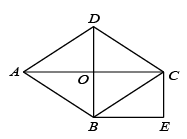
如图，在平面直角坐标系中，菱形的顶点在反比例函数图象上，直线交于点，交正半轴于点，且求的长：若，求的值．

1. 如图，在平面直角坐标系中，菱形 $\text{[math]}$ 的顶点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 图象上，直线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 正半轴于点 $\text{[math]}$ ，且 $\text{[math]}$

$\text{[math]}$ 求 $\text{[math]}$ 的长：

$\text{[math]}$ 若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．

【考点】

勾股定理; 菱形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 若菱形 $\text{[math]}$ 的两条对角线的长分别为12和16，则菱形 $\text{[math]}$ 的周长为．

填空题容易

2. 明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，踏板一尺离地．送行二步恰竿齐，五尺板高离地…”翻译成现代文为：如图，秋千 $\text{[math]}$ 静止的时候，踏板离地高一尺（ $\text{[math]}$ 尺），将它往前推进两步（ $\text{[math]}$ 尺），此时踏板升高离地五尺（ $\text{[math]}$ 尺），求秋千绳索（ $\text{[math]}$ 或 $\text{[math]}$ ）的长度．

综合题容易

3. 在△ABC中，∠C=30°，AC=4cm，AB=3cm，求BC的长.

解答题容易