1.
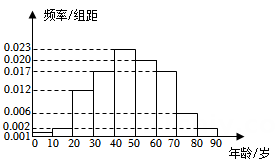
2023年国庆节假期期间,某超市举行购物抽奖赢手机的活动.活动规则如下:在2023年9月29日至10月6日期间消费金额(单位:元)不低于100元的顾客获得一张奖券(假设每名顾客只消费一次),奖券尾数随机生成,尾数为奇数和偶数的奖券数量相同,若顾客的奖券尾数为奇数,则获得一份价值5元的礼品,若顾客的奖券尾数为偶数,则获得抽取价值6999元的手机的资格.根据统计,顾客进入该超市消费金额的频率分布直方图如图所示.

以样本估计总体,以频率估计概率.
(1)
若有1000名购物的顾客,求送出的礼品的价值金额;
(2)
若超市计划投入的活动经费(购买手机的费用与发放的购物券金额总和)不超过顾客消费总金额的10%(同一组中的数据用该组区间的中点值为代表),求每1000名顾客最多送出多少部手机.
【考点】
频率分布直方图;
众数、中位数、平均数;
能力提升
真题演练