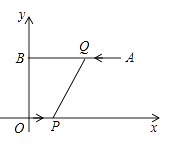1.
如图1,已知直线 交y轴、x轴于点
交y轴、x轴于点 , 点
, 点 . 直线
. 直线 :
: 交直线
交直线 于点P.点G为x轴上一点,过点G作x轴的垂线交直线
于点P.点G为x轴上一点,过点G作x轴的垂线交直线 ,
,  于E,F两点.
于E,F两点.

(1)
求直线 的函数表达式.
(2)
如图1,若点P到y轴距离与到直线
的函数表达式.
(2)
如图1,若点P到y轴距离与到直线 的距离相等,求点G的坐标.
(3)
在(2)的条件下,如图2,点M为y正半轴上一个动点,设点M的坐标
的距离相等,求点G的坐标.
(3)
在(2)的条件下,如图2,点M为y正半轴上一个动点,设点M的坐标 , 连结
, 连结 , 将线段
, 将线段 绕点M顺时针旋转
绕点M顺时针旋转 得线段
得线段 , 连接
, 连接 , 若点M在运动过程中
, 若点M在运动过程中 始终在
始终在 的内部(包括边界),求m的取值范围.
的内部(包括边界),求m的取值范围.
【考点】
一次函数中的动态几何问题;
能力提升
真题演练