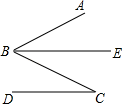
1.
完成下面的证明过程.
已知:如图, ,
平分
,
平分
.
求证: .
证明:∵(已知),
∴( _________________________ ).
∵(已知),
∴________
( ___________________________ ).
又∵平分
,
平分
(已知),
∴(角平分线的定义),
∴ ,
∴ ,
∴ , 即
.

【考点】
平行线的性质;
角平分线的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练