1.
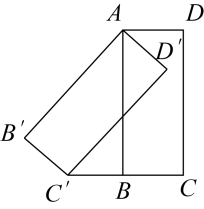
如图, 是等边三角形,点
是等边三角形,点 在
在 边上,将
边上,将 绕点
绕点 旋转得到
旋转得到 .
.

(1)
求证: 是等边三角形
(2)
若
是等边三角形
(2)
若 , 求
, 求 的周长.
的周长.
【考点】
等边三角形的判定与性质;
旋转的性质;