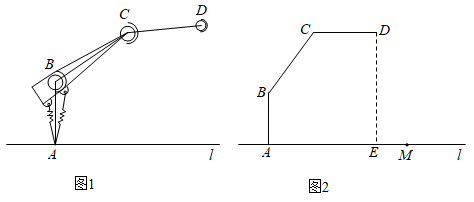
姑婆山国家森林公园古窑冲猴趣园，调皮可爱的猴子随处可见．如图：有两只猴子爬到—棵树上的点B处，且，突然发现远方A处有好吃的东西，其中一只猴子沿树爬下走到离树处的池塘A处，另一只猴子先爬到树顶D处后再沿缆绳线段滑到A处，已知两只猴子所经过的路程相等，设为．

1. 姑婆山国家森林公园古窑冲猴趣园，调皮可爱的猴子随处可见．如图：有两只猴子爬到—棵树 $\text{[math]}$ 上的点B处，且 $\text{[math]}$ ，突然发现远方A处有好吃的东西，其中一只猴子沿树爬下走到离树 $\text{[math]}$ 处的池塘A处，另一只猴子先爬到树顶D处后再沿缆绳线段 $\text{[math]}$ 滑到A处，已知两只猴子所经过的路程相等，设 $\text{[math]}$ 为 $\text{[math]}$ ．

(1) 请用含有x的整式表示线段 $\text{[math]}$ 的长为 m；

(2) 求这棵树高有多少米？

【考点】

勾股定理的应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 一架方梯AB长25米，如图所示，斜靠在一面上：

(1) 若梯子底端离墙7米，这个梯子的顶端距地面有多高？

(2) 在（1）的条件下，如果梯子的顶端下滑了4米，那么梯子的底端在水平方向滑动了几米？

综合题普通

2. 如图，一架梯子 $\text{[math]}$ 长13米，斜靠在一面墙上，梯子底端离墙5米．

(1) 这个梯子的顶端距地面有多高？

(2) 如果梯子的顶端下滑了5米，那么梯子的底端在水平方向滑动了多少米？

综合题普通

3. 如图，直线l为一条公路，A，D两处各有一个村庄， $\text{[math]}$ 于点B， $\text{[math]}$ 于点C， $\text{[math]}$ 千米， $\text{[math]}$ 千米， $\text{[math]}$ 千米．现需要在 $\text{[math]}$ 上建立一个物资调运站E，使得E到A，D两个村庄距离相等，请求出E到C的距离．

综合题普通