1.
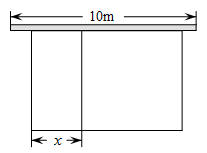
如图,某农场有两堵互相垂直的墙,长度分别为 米和
米和 米.该农场打算借这两堵墙建一个长方形饲养场
米.该农场打算借这两堵墙建一个长方形饲养场 , 用总长
, 用总长 米的木栏围成,中间预留1米宽的通道,在
米的木栏围成,中间预留1米宽的通道,在 和
和 边上各留1米宽的门,设
边上各留1米宽的门,设 长x米.
长x米.

(1)
写出 的长(用含x的代数式表示).
(2)
若饲养场
的长(用含x的代数式表示).
(2)
若饲养场 的面积为
的面积为 平方米,求x的值.
平方米,求x的值.
【考点】
一元二次方程的应用-几何问题;
能力提升
真题演练