1.
乘法公式的探究及应用.

(1)
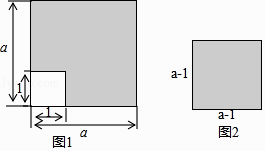
如图 1, 可以求出阴影部分的面积是 . (写成两数平方差的形式)
(2)
如图 2, 若将阴影部分裁剪下来, 重新拼成一个矩形, 它的宽是 , 长是, 面积是 . (写成多项式乘法的形式)
(3)
比较图 1、图 2 两图的阴影部分面积, 可以得到乘法公式: . (用等式表示)
【考点】
平方差公式的几何背景;