1.
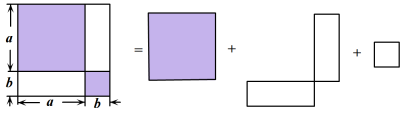
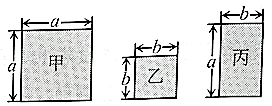
几何验证:如图1,可验证公式(a+b)2=a2+2ab+b2.

(1)
公式应用:若 ,
,  , 则m2+n2的值为;
(2)
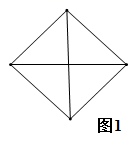
拓展延伸:如图2,四边形
, 则m2+n2的值为;
(2)
拓展延伸:如图2,四边形 和四边形
和四边形 是两个正方形,若
是两个正方形,若 ,
,  , 则
, 则 的值为.
的值为.

图2
【考点】
完全平方公式的几何背景;
能力提升
真题演练