1.
数学模型可以用来解决一类问题,是数学应用的基本途径,通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.

(1)
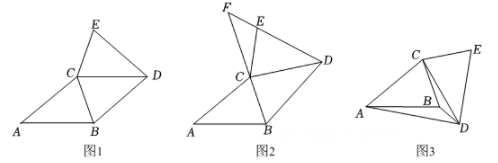
发现问题:如图1,在 和
和 中,
中, ,
,  ,
,  , 连接
, 连接 , 延长
, 延长 交
交 于点D.则
于点D.则 与
与 的数量关系:,
的数量关系:,
 ;
(2)
类比探究:如图2,在
;
(2)
类比探究:如图2,在 和
和 中,
中, ,
,  ,
,  , 连接
, 连接 , 延长
, 延长 交
交 于点D.请猜想
于点D.请猜想 与
与 的数量关系及
的数量关系及 的度数,并说明理由;
(3)
拓展延伸:如图3,
的度数,并说明理由;
(3)
拓展延伸:如图3, 和
和 均为等腰直角三角形,
均为等腰直角三角形, , 连接
, 连接 , 且点B,E,F在一条直线上,过点A作
, 且点B,E,F在一条直线上,过点A作 , 垂足为点M.请猜想
, 垂足为点M.请猜想 之间的数量关系并说明理由.
之间的数量关系并说明理由.
【考点】
等腰三角形的性质;
三角形全等的判定-SAS;