0 返回出卷网首页
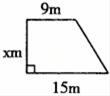
1. 李大伯在一面靠水渠边，用篱笆围成-块直角梯形浆地（ 如图所示）。已知篱笆总长度是36米。篱笆怎样围成这块菜地的面积最大？最大的面积是多少平方米？

【考点】
梯形的面积;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
解决问题 普通
基础巩固
能力提升
变式训练
拓展培优
真题演练
换一批
1. 有一块梯形钢板，上底是2.4米，下底是3.6米，高是2米，这块梯形钢板的面积是多少平方米？
解决问题 容易