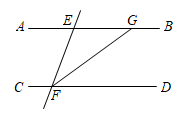
【实践活动】如图1，将一副三角板的直角顶点重合摆放．（1）与的大小关系是______ ． (填“”“”或“”)（2）与之间的数量关系是_____

1. 【实践活动】

如图1，将一副三角板的直角顶点重合摆放．

（1） $\text{[math]}$ 与 $\text{[math]}$ 的大小关系是 $\text{[math]}$ ______ $\text{[math]}$ ． (填“ $\text{[math]}$ ”“ $\text{[math]}$ ”或“ $\text{[math]}$ ”)

（2） $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系是______．

【拓展探究】

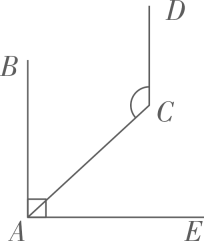
（3）如图2，若 $\text{[math]}$ ，且 $\text{[math]}$ ，探索 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系，并说明理由．

【考点】

角的运算;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题普通

基础巩固

能力提升

变式训练

拓展培优

真题演练

换一批

解答题容易

填空题容易

（1）如图1，若点D在AB上，则∠EBC的度数为　　；

（2）如图2，若∠EBC＝170°，则∠α的度数为　　；

（3）如图3，若∠EBC＝118°，求∠α的度数；

（4）如图3，若0°＜∠α＜60°，求∠ABE－∠DBC的度数．

解答题容易

综合与探究
素材1	如图1，O是弹力墙MN 上一点，魔法棒从OM的位置开始绕点O 向ON 的位置顺时针旋转，当转到ON位置时，则从ON位置弹回，继续向OM位置旋转；当转到OM位置时，再从OM 的位置弹回，继续转向 ON位置⋯⋯如此反复.按照这种方式将魔法棒进行如下步骤的旋转(如图2)：第1步，从OA。(OA₀在OM上)开始旋转α至OA₁；第2步，从 OA₁开始继续旋转2α至OA₂；第3步，从 OA₂ 开始继续旋转3α至OA₃……
素材2	例如：当α=30°时，OA₁ ， OA₂ ， OA₃ ， OA₄的位置如图2所示，其中OA₃恰好落在ON上，∠A₃OA₄=120°；当α=20°时，OA₁ ， OA₂ ， OA₃ ， OA₄ ， OA₅的位置如图3 所示，其中第4 步旋转到 ON后弹回，即∠A₃ON+∠NOA₄=80°，而 OA₅恰好与OA₂ 重合.
问题解决
问题1	(1)若α=35°，在图4中借助量角器画出OA₂ ， OA₃ ，其中∠A₃OA₂ 的度数为 °.
问题2	(2)若α<30°，且OA₁所在的射线平分∠A₂OA₃ ，在如图5 中画出OA₁ ， OA₂ ， OA₃ ， OA₄并求出α的值.
问题3	(3)若α<36°，且∠A₂OA₄=20°，则对应的α的值是 .
问题4	(4)当OA；所在的射线是∠A，OAₖ(i，j，k是正整数，且OAⱼ 与OAₖ不重合)的平分线时，旋转停止，请探究：对于任意角α(α的度数为正整数，且α<180°)，旋转是否可以停止? 写出你的探究思路.