1.
综合与实践.
【问题情境】
如图(1),等腰直角三角形CAB和等腰直角三角形CED的直角顶点重合,
.将
绕点
顺时针旋转
, 连接AE,BD,延长AE交射线BD于点
.

(1)
【猜想证明】
(2)
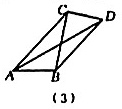
如图(3),在△CED旋转的过程中,连接CF,探究AF,BF,CF之间的数量关系.
(3)
【拓展应用】
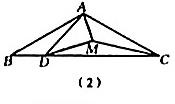
如图(2),当时,判断四边形CDFE的形状,并说明理由.
在△CED旋转的过程中,若 , 请直接写出CF的长度.
【考点】
正方形的判定;
三角形的综合;
手拉手全等模型;
四点共圆模型;
能力提升