1.
如图1，已知正方形ABCD的边长为1，点P是AD边上的一个动点，点A关于直线BP的对称点是点Q ， 连接PQ、DQ、CQ、BQ ， 设
．
(1)
的最小值是；此时x的值是．
(2)
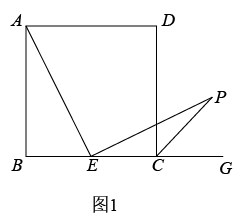
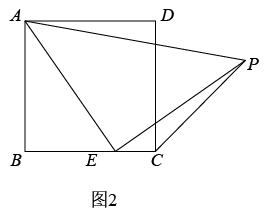
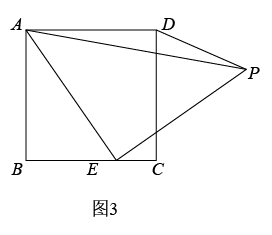
如图2，若PQ的延长线交CD边于点E ， 并且
．
(3)
如图2，若PQ的延长线交CD边于点E ， 求线段PE的最小值．
①求证：点E是CD的中点：②求x的值．
【考点】
等腰三角形的性质;
正方形的性质;
轴对称的应用-最短距离问题;
