1.
如图是由小正方形组成的 网格,每个小正方形的顶点叫做格点.A , B , C , E , F都是格点,N在
网格,每个小正方形的顶点叫做格点.A , B , C , E , F都是格点,N在 上,M在
上,M在 上,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
上,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)
在图(1)中,先以 ,
,  为邻边作平行四边形
为邻边作平行四边形 , 再在
, 再在 上画点H , 使得
上画点H , 使得 ;
(2)
在图(2)中,先画点F关于
;
(2)
在图(2)中,先画点F关于 的对称点P , 再过点M作
的对称点P , 再过点M作 的平行线l.
的平行线l.
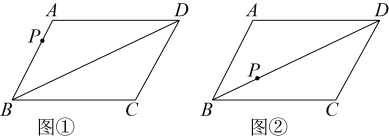
图(1)
图(2)
【考点】
三角形全等的判定;
平行四边形的判定与性质;
作图﹣轴对称;
能力提升