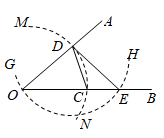
如图，在平面直角坐标系中，直线与双曲线交于A、B两点，其中A的坐标为， D是以点为圆心，半径长为1的圆上一动点，连接， E为的中点.

1. 如图，在平面直角坐标系中，直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 交于A、B两点，其中A的坐标为 $\text{[math]}$ ， D是以点 $\text{[math]}$ 为圆心，半径长为1的圆上一动点，连接 $\text{[math]}$ ， E为 $\text{[math]}$ 的中点.

(1) 求直线和双曲线的解析式；

(2) 求线段 $\text{[math]}$ 长度的最小值．

【考点】

圆的相关概念;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 定义：在平面直角坐标系中，图形 G 上点 P（x，y）的纵坐标 y 与其横坐标 x 的差 y﹣x 称为 P 点的“坐标差”，而图形 G 上所有点的“坐标差”中的最大值称为图形 G 的“特征值”．

(1) ①点 A（1，3）的“坐标差”为；

②抛物线 $\text{[math]}$ 的“特征值”为；

(2) 某二次函数 $\text{[math]}$ 的“特征值”为﹣1，点 B（m，0）与点 C 分别是此二次函数的图象与 x 轴和 y 轴的交点，且点 B 与点 C 的“坐标差”相等．

①直接写出 m＝；（用含 c 的式子表示）

②求此二次函数的表达式．

(3) 如图，在平面直角坐标系 xOy 中，以 M（2，3）为圆心，2 为半径的圆与直线 y＝x 相交于点 D、E，请直接写出⊙M 的“特征值”为．

解答题困难

2. 定义：在平面直角坐标系中，图形 G 上点 P（x，y）的纵坐标 y 与其横坐标 x 的差 y﹣x 称为 P 点的“坐标差”，而图形 G 上所有点的“坐标差”中的最大值称为图形 G 的“特征值”．

(1) ①点 A（1，3）的“坐标差”为；

②抛物线 $\text{[math]}$ 的“特征值”为；

(2) 某二次函数 $\text{[math]}$ 的“特征值”为﹣1，点 B（m，0）与点 C 分别是此二次函数的图象与 x 轴和 y 轴的交点，且点 B 与点 C 的“坐标差”相等．

①直接写出 m＝；（用含 c 的式子表示）

②求此二次函数的表达式．

(3) 如图，在平面直角坐标系 xOy 中，以 M（2，3）为圆心，2 为半径的圆与直线 y＝x 相交于点 D、E，请直接写出⊙M 的“特征值”为．

解答题困难

3. 已知线段AB=3cm，用图形表示到点A的距离小于2cm，且到点B的距离大于2cm的所有点的集合．

解答题普通