1.
掷一枚质地均匀的骰子,记事件 “出现的点数不超过3”,事件
“出现的点数不超过3”,事件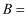 “出现的点数是3或5”,事件
“出现的点数是3或5”,事件 “出现的点数是偶数”,则事件
“出现的点数是偶数”,则事件 、
、 与
与 的关系为( )
的关系为( )
A.
事件 与
与 互斥
B.
事件
互斥
B.
事件 与
与 对立
C.
事件
对立
C.
事件 与
与 独立
D.
事件
独立
D.
事件 与
与 独立
独立
【考点】
相互独立事件;
基础巩固
能力提升
变式训练
拓展培优
真题演练
