1.
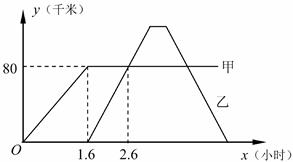
“低碳生活,绿色出行”的理念正逐渐被人们所接受,越来越多的人选择骑自行车上出行.小星某天骑自行车上班从家出发到图书馆的过程中行进速度v(米/分)随时间 (分钟)变化的函数图象大致如图所示,图象由三条线段
(分钟)变化的函数图象大致如图所示,图象由三条线段 和
和 组成.设线段
组成.设线段 上有一动点
上有一动点 , 直线l过点
, 直线l过点 且与横轴垂直,梯形
且与横轴垂直,梯形 在直线l左侧部分的面积即为
在直线l左侧部分的面积即为 分钟内小星行进的路程(米).
分钟内小星行进的路程(米).

(1)
①当 分钟时,速度
分钟时,速度 ▲ 米/分钟,路程
▲ 米/分钟,路程 ▲ 米;
(2)
当
▲ 米;
(2)
当 和
和 时,分别求出路程
时,分别求出路程 (米)关于时间t(分钟)的函数解析式;
(米)关于时间t(分钟)的函数解析式;
②当分钟时,速度
▲ 米/分钟,路程
▲ 米.
【考点】
一次函数的实际应用;
能力提升
真题演练