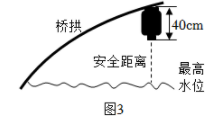
如图，平面直角坐标系中，桥孔抛物线对应的二次函数关系式是y＝﹣x2 ，桥下的水面宽AB为6m，当水位上涨2m时，水面宽CD为m（结果保留根号）．

0 返回首页

1. 如图，平面直角坐标系中，桥孔抛物线对应的二次函数关系式是y＝﹣ $\text{[math]}$ x² ，桥下的水面宽AB为6m，当水位上涨2m时，水面宽CD为m（结果保留根号）．

【考点】

二次函数的实际应用-拱桥问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题普通

基础巩固

能力提升

变式训练

拓展培优

真题演练

换一批

1. 廊桥是我国古老的文化遗产．如图，是某座抛物线型的廊桥示意图，已知抛物线的函数表达式为 $\text{[math]}$ ，为保护廊桥的安全，在该抛物线上距水面AB高为8米的点E，F处要安装两盏警示灯，则这两盏灯的水平距离EF是米．（精确到1米）

填空题容易

2. 如图所示，桥拱是抛物线形，其函数解析式是 $\text{[math]}$ ，当水位线在 $\text{[math]}$ 位置时，水面宽为12米，这时水面离桥顶的高度 $\text{[math]}$ 是米．

填空题容易

1. 如图是抛物线型拱桥，当拱顶离水面2m时，水面宽4m，水面下降2m，水面宽度增加m.

填空题普通

2. 廊桥是我国古老的文化遗产，如图是某座抛物线形的廊桥示意图．已知抛物线的函数表达式为 $\text{[math]}$ ，为保护廊桥的安全，在该抛物线上距水面 $\text{[math]}$ 高为6米的点E，F处要安装两盏警示灯，则这两盏灯的水平距离 $\text{[math]}$ 是米．

填空题普通

3. 如图是一个横断面为抛物线形状的拱桥，当水面宽 $\text{[math]}$ 米时，拱顶（拱桥洞的最高点）离水面 $\text{[math]}$ ，水面上升 $\text{[math]}$ 时，水面的宽度为．

填空题普通

1. 廊桥是我国古老的文化遗产．如图是某座抛物线形廊桥的示意图，已知水面AB宽48m，拱桥最高处点C到水面 $\text{[math]}$ 的距离为12m，为保护该桥的安全，现要在该抛物线上的点E，F处安装两盏警示灯，若要保证两盏灯的水平距离 $\text{[math]}$ 是24m，则警示灯E距水面 $\text{[math]}$ 的高度为（）

A. 12m B. 11m C. 10m D. 9m

单选题普通

2. 根据以下素材，探索完成任务

如何设计拱桥上救生圈的悬挂方案?
素材1	图1是一座抛物线形拱桥，以抛物线两个水平最低点连线为x轴，抛物线离地面的最高点的铅垂线为y轴建立平面直角坐标系，如图2所示．某时测得水面宽 $\text{[math]}$ ，拱顶离水面最大距离为10m，抛物线拱形最高点与x轴的距离为5m．据调查，该河段水位在此基础上再涨1m达到最高．
素材2	为方便救助溺水者，拟在图1的桥拱上方栏杆处悬挂救生圈，如图3，救生圈悬挂点为了方便悬挂，救生圈悬挂点距离抛物线拱面上方1m，且相邻两救生圈悬挂点的水平间距为4m．为美观，放置后救生圈关于y轴成轴对称分布．（悬挂救生圈的柱子大小忽略不计）
问题解决
任务1	确定桥拱形状	根据图2，求抛物线的函数表达式．
任务2	拟定设计方案	求符合悬挂条件的救生圈个数，并求出最右侧一个救生圈悬挂点的坐标．
任务3	探究救生绳长度	当水位达到最高时，上游个落水者顺流而下到达抛物线拱形桥面的瞬间，若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边，求救生绳至少需要多长．（救生圈大小忽略不计，结果保留整数）

实践探究题普通

3. 河北省赵县的赵州桥的桥拱是近似的抛物线形，建立如图所示的平面直角坐标系，其函数的关系式为y=﹣ $\text{[math]}$ x² ，当水面离桥拱顶的高度DO是4m时，这时水面宽度AB为（）

A. ﹣20m B. 10m C. 20m D. ﹣10m

单选题普通

1. 图1为广安某新建公园的抛物线形拱桥，图2是其横截面示意图，测得水面宽度 $\text{[math]}$ 米时，拱顶离水面的距离为 $\text{[math]}$ 米．

当地政府拟在公园投放游船供游客乘坐，图3是游船载重最少时的横截面示意图，露出水面的船身为矩形 $\text{[math]}$ ，船顶为等腰三角形 $\text{[math]}$ ．测得相关数据如下： $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米．为确保安全，拟在桥底P，Q两处设置航行警戒线，要求：

①游船底部HI在点P，Q之间通行；

②载重最少时，游船顶部E与拱桥的竖直距离至少为0.5米．若以 $\text{[math]}$ 所在直线为 $\text{[math]}$ 轴，点D为原点建立直角坐标系，请解答以下问题：

(1) 求这条抛物线的函数表达式；

(2) 求警戒线之间宽度 $\text{[math]}$ 的最大值．（当 $\text{[math]}$ 最大时，船身H与P重合，或I与Q重合）

综合题普通

2. 根据以下素材，完成设计货船通过双曲线桥的方案：一座曲线桥如图1所示，当水面宽 $\text{[math]}$ 米时，桥洞顶部离水面距离 $\text{[math]}$ 米．已知桥洞形如双曲线，图2是其示意图，且该桥关于CD对称．如图4，一艘货船露出水面部分的横截面为矩形EFGH ，测得 $\text{[math]}$ 米．因水深足够，货船可以根据需要运载货物．据调查，船身下降的高度h（米）与货船增加的载重量t（吨）满足函数表达式 $\text{[math]}$ ．

(1) 问题解决：确定桥洞的形状．

建立平面直角坐标系如图3所示，CD落在第一象限的角平分线上．设点C为 $\text{[math]}$ ，

①点A的坐标为 ▲ ．（用m的代数式表示）；

②求出经过点A的双曲线的函数表达式．

(2) 探索应用：

这艘货船运载货物高3米（即 $\text{[math]}$ 米），此时货船能通过该桥洞吗?

若能，请说明理由；若不能，至少要增加多少吨货物?（已知 $\text{[math]}$ ， $\text{[math]}$ ．）

实践探究题困难

3. 某地欲搭建一桥，桥的底部两端间的距离AB=L称跨度，桥面最高点到AB的距离CD=h称拱高，当L和h确定时，有两种设计方案可供选择：①抛物线型：②）圆弧型，已知这座桥的跨度L=20米，拱高h=5米.

(1) 如图1，若设计成抛物线型，以AB所在直线为x轴，B的垂直平分线为y轴建立坐标系，求此函数表达式；

(2) 如图2，若设计成圆弧型，求该圆弧所在圆的半径；

(3) 现有一艘宽为15米的货船，船舱顶部为方形，并高出水面2.2米，从以上两种方案中，任选一种方案，判断此货船能否顺利通过你所选方案的桥?并说明理由.

综合题普通

1. 三孔桥横截面的三个孔都呈抛物线形，两小孔形状、大小完全相同．当水面刚好淹没小孔时，大孔水面宽度为10米，孔顶离水面1.5米；当水位下降，大孔水面宽度为14米时，单个小孔的水面宽度为4米，若大孔水面宽度为20米，则单个小孔的水面宽度为（）

A. 4 $\text{[math]}$ 米 B. 5 $\text{[math]}$ 米 C. 2 $\text{[math]}$ 米 D. 7米

单选题普通

2. 如图是抛物线形拱桥，当拱顶离水面2米时，水面宽6米，水面下降米，水面宽8米.

填空题普通

3. 根据以下素材，探索完成任务．

如何设计拱桥景观灯的悬挂方案？
素材1	图1中有一座拱桥，图2是其抛物线形桥拱的示意图，某时测得水面宽 20m ，拱顶离水面 5m ．据调查，该河段水位在此基础上再涨 1.8m 达到最高．
素材2	为迎佳节，拟在图1桥洞前面的桥拱上悬挂 40cm 长的灯笼，如图3．为了安全，灯笼底部距离水面不小于 1m ；为了实效，相邻两盏灯笼悬挂点的水平间距均为 1.6m ；为了美观，要求在符合条件处都挂上灯笼，且挂满后成轴对称分布．
问题解决
任务1	确定桥拱形状	在图2中建立合适的直角坐标系，求抛物线的函数表达式．
任务2	探究悬挂范围	在你所建立的坐标系中，仅在安全的条件下，确定悬挂点的纵坐标的最小值和横坐标的取值范围．
任务3	拟定设计方案	给出一种符合所有悬挂条件的灯笼数量，并根据你所建立的坐标系，求出最左边一盏灯笼悬挂点的横坐标．

实践探究题普通