1.
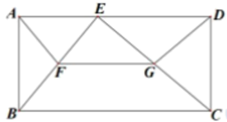
某社区为了让居民享受更多“开窗见景,推门见绿”的空间,决定将一块四边形区域改造为儿童游乐场.图1是该区域的设计图,图2是该四边形区域的几何示意图, ,
,  ,
,  ,
,  ,
,  , 按照计划要先在该区域铺设塑胶,已知铺设1平方米塑胶需要200元,则铺满该区域需要的费用是( )
, 按照计划要先在该区域铺设塑胶,已知铺设1平方米塑胶需要200元,则铺满该区域需要的费用是( )

A.
40800元
B.
91600元
C.
60800元
D.
48000元
【考点】
勾股定理;
勾股定理的逆定理;
基础巩固
能力提升
变式训练
拓展培优
真题演练