如图在△ABD和△ACE都是等边三角形，则△ADC≌△ABE的根据是（）

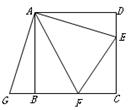
1. 如图在△ABD和△ACE都是等边三角形，则△ADC≌△ABE的根据是（）

A. SSS B. SAS C. ASA D. AAS

【考点】

三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题容易

1. 数学兴趣小组要利用所学知识，自己制作一个工具测量一个锥形瓶的内径．如图，用螺丝钉将两根木棒 $\text{[math]}$ ， $\text{[math]}$ 的中点固定，利用全等三角形知识，测得 $\text{[math]}$ 的长就是锥形瓶内径 $\text{[math]}$ 的长．其中，判定 $\text{[math]}$ 和 $\text{[math]}$ 全等的方法是（）

A. SSS B. ASA C. SAS D. AAS

单选题容易

2. 如图，△ABC≌△DEC，CA和CD，CB和CE是对应边，点E在线段AB上，若∠AED+∠BCE=52°，则∠ACD的大小为（　　）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 如图，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则判定 $\text{[math]}$ 的方法是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易