1.
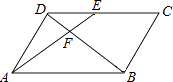
如图,在 中,点D,E,F分别在边
中,点D,E,F分别在边 ,
,  ,
,  上,连接
上,连接 ,
,  . 已知四边形
. 已知四边形 是平行四边形,
是平行四边形, .
.

(1)
若 , 求线段
, 求线段 的长.
(2)
若
的长.
(2)
若 的面积为3,求平行四边形
的面积为3,求平行四边形 的面积.
的面积.
【考点】
平行四边形的性质;
相似三角形的判定与性质;