1.
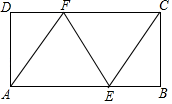
如图1,在平面直角坐标系中,矩形 的顶点
的顶点 在
在 轴上,顶点
轴上,顶点 在
在 轴上,已知点
轴上,已知点 ,
,  , 且
, 且 ,
,  是关于
是关于 的方程.
的方程.  的两个根
的两个根  , 点
, 点 是
是 的中点,连接
的中点,连接 .
.

(1)
求点 的坐标;
(2)
若反比例函数
的坐标;
(2)
若反比例函数  的图象经过点
的图象经过点 , 点
, 点 为
为 轴上一点,点
轴上一点,点 为反比例函数图象上一点,是否存在点
为反比例函数图象上一点,是否存在点 , 使以
, 使以 ,
,  ,
,  ,
,  为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标,若不存在,请说明理由;
(3)
如图
的坐标,若不存在,请说明理由;
(3)
如图 , 在线段
, 在线段 上取点
上取点 , 使得
, 使得 ,
,  是线段
是线段 上的一动点,
上的一动点,  是双曲线
是双曲线 与线段
与线段 的交点,且满足,
的交点,且满足, , 当
, 当 取得最小值时,求
取得最小值时,求 的值.
的值.
【考点】
勾股定理;
平行四边形的性质;
矩形的性质;
能力提升
真题演练