1.
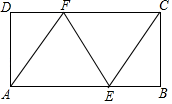
操作体验:如图,在矩形ABCD中,点E、F分别在边AD、BC上,将矩形ABCD沿直线EF折叠,使点D恰好与点B重合,点C落在点C′处.点P为直线EF上一动点(不与E、F重合),过点P分别作直线BE、BF的垂线,垂足分别为点M和N , 以PM、PN为邻边构造平行四边形PMQN.

(1)
如图1,求证:BE=BF;
(2)
特例感知:如图2,若DE=5,CF=2,当点P在线段EF上运动时,求平行四边形PMQN的周长;
(3)
类比探究:若DE=a , CF=B.
①如图3,当点P在线段EF的延长线上运动时,试用含a、b的式子表示QM与QN之间的数量关系,并证明;
②如图4,当点P在线段FE的延长线上运动时,请直接用含a、b的式子表示QM与QN之间的数量关系.(不要求写证明过程)
【考点】
勾股定理;
平行四边形的性质;
矩形的性质;
能力提升
真题演练