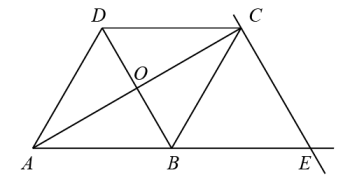
1.
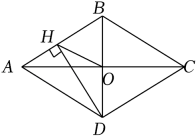
如图,四边形ABCD是菱形,∠DAB=48°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO=度.

【考点】
菱形的性质;
直角三角形斜边上的中线;
基础巩固
能力提升
变式训练
拓展培优
真题演练