1.
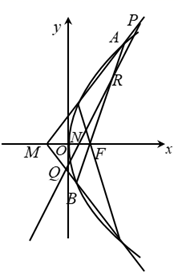
如图,已知椭圆 和抛物线
和抛物线 ,
,  的焦点
的焦点 是
是 的上顶点,过
的上顶点,过 的直线交
的直线交 于
于 、
、 两点,连接
两点,连接 、
、 并延长之,分别交
并延长之,分别交 于
于 、
、 两点,连接
两点,连接 , 设
, 设 、
、 的面积分别为
的面积分别为 、
、 .
.
(1)
求 的值;
(2)
求
的值;
(2)
求 的值;
(3)
求
的值;
(3)
求 的取值范围.
的取值范围.
【考点】
抛物线的标准方程;
直线与圆锥曲线的综合问题;