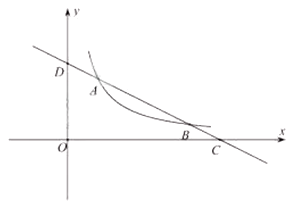
1.
在平面直角坐标系 中,二次函数
中,二次函数 的图象经过点
的图象经过点 .
.
(1)
求该二次函数的解析式以及图象顶点的坐标;
(2)
一次函数 的图象经过点A,点
的图象经过点A,点 在一次函数
在一次函数 的图象上,点
的图象上,点 在二次函数
在二次函数 的图象上,若
的图象上,若 , 求m的取值范围.
, 求m的取值范围.
【考点】
待定系数法求一次函数解析式;