1.
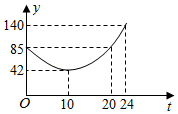
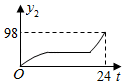
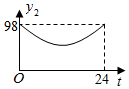
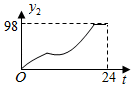
A,B两地之间有一快递中转站C,且它们在同一直线上.快递员甲、乙骑电动车分别从A地、B地同时出发以各自的速度匀速前往中转站C地取货.恰好两人同时到达C地.取货后(取货时间忽略不计)各自沿原路线原速返回,返回途中甲突然想起乙拿错一件快递,于是甲立即掉头以原来速度的3倍追及乙,乙一直保持原速返回B地,经过一段时间,甲赶上乙后,两人立即以甲提速后的速度一起前往中转站C核对信息.已知乙的速度为15千米/时.在此过程中,甲、乙两人距C地的距离和为y(单位:千米)与出发时间x(单位:小时)之间的关系如图所示.

请根据图中的信息解决下列问题:
(1)
填空: 两地距离为______千米,
两地距离为______千米, ______;
(2)
当快递员甲追上快递员乙时,他们距中转站C地多少千米?
(3)
当两人相距3千米,请直接写出x的值.
______;
(2)
当快递员甲追上快递员乙时,他们距中转站C地多少千米?
(3)
当两人相距3千米,请直接写出x的值.
【考点】
函数的图象;
通过函数图象获取信息;
能力提升
真题演练