1.
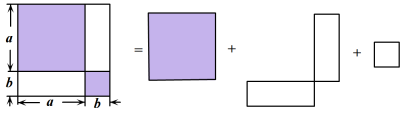
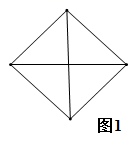
如图,2002年8月在北京召开的国际数学家大会会标其原型是我国古代数学家赵爽的《勾股弦图》,它是由四个全等的直角三角形拼接而成.如果大正方形的面积是16,直角三角形的直角边长分别为 , 且
, 且 , 那么图中小正方形的面积是( )
, 那么图中小正方形的面积是( )

A.
2
B.
3
C.
4
D.
5
【考点】
完全平方公式的几何背景;
基础巩固
能力提升
变式训练
拓展培优
真题演练