1.
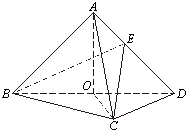
如图,在矩形纸片 中,
中, , 沿
, 沿 将
将 折起,使点
折起,使点 到达点
到达点 的位置,点
的位置,点 在平面
在平面 的射影
的射影 落在边
落在边 上.
上.

(1)
求 的长度;
(2)
若
的长度;
(2)
若 使棱
使棱 上的一个动点,是否存在点
上的一个动点,是否存在点 , 使得平面
, 使得平面 与平面
与平面 夹角的余弦值为
夹角的余弦值为 ?若存在,求出
?若存在,求出 的长度;若不存在,说明理由.
的长度;若不存在,说明理由.
【考点】
与二面角有关的立体几何综合题;